What are the differences between raster-scan CRTs and random-access or vector CRTs? [4]
Raster-scan system:-
1)raster displays have less resolution.
2)the lines produced are zig-zag as the plotted values are discrete.
3)high degree realism is achieved in picture with the aid of advanced shading and hidden surface technique.
4)decreasing memory costs have made raster systems popular.
Random scan system:-
1)random displays have high resolutions since the picture defination is stored as a set of line drawing commands and not as a set of intensity values.
2)smooth lines are produced as the electron beam directly follows the line path.
3)realism is difficult to achieve.
4)random-scan system's are generally costlier.
a) Explain why RGB color model is used for display. How different shades of colors are generated on the RGB monitors. [6]
The RGB color model creates colors by mixing light, red, green and blue. All video displays are RGB. Since it is impossible to print a light mixture printers are able to simulate full color by using four colors, cyan, magenta, yellow and black. Most new color laser copy machines automatically convert RGB to CMYK when a digital file is sent, but the results may be off color.
1. e) Explain how colour images are displayed on a computer monitor. [4]
2.3 CRTs for Color Display
This was one the earlier CRTs to produce color displays. Coating phosphors of different compounds can produce different colored pictures. But the basic problem of graphics is not to produce a picture of a predetermined color, but to produce color pictures, with the color characteristics chosen at run time. The basic principle behind colored displays is that combining the 3 basic colors –Red, Blue and Green, can produce every color. By choosing different ratios of these three colors we can produce different colors – millions of them in-fact. We also have basic phosphors, which can produce these basic colors. So, one should have a technology to combine them in different combinations.
2.4 Beam Penetration CRT
This CRT is similar to the simple CRT, but it makes use of multi coloured phosphorus of number of layers. Each phosphorus layer is responsible for one colour. All other arrangements are similar to simple CRT. It can produce a maximum of 4 to 5 colours The organization is something like this - The red, green and blue phosphorus are coated in layers - one behind the other. If a low speed beam strikes the CRT, only the red colored phosphorus is activated, a slightly accelerated beam would activate both red and green (because it can penetrate deeper) and a much more activated one would add the blue component also. But the basic problem is a reliable technology to accelerate the electronic beam to precise levels to get the exact colors - it is easier said than done. However, a limited range of colors can be conveniently produced using the concept.
c) Explain shadow masking method for colour monitor. [4]
The shadow mask CRT, instead of using one electron gun, uses 3 different guns placed one by the side of the other to form a triangle or a "Delta" as shown. Each pixel point on the screen is also made up of 3 types of phosphors to produce red, blue and green colors. Just before the phosphor screen is a metal screen, called a "shadow mask". This plate has holes placed strategically, so that when the beams from the three electron guns are focused on a particular pixel, they get focused on particular color producing pixel only i.e. If for convenience sake we can call the electronic beams as red, blue and
green beams (though in practice the colors are produced by the phosphors, and until the beams hit the phosphor dots, they produce no colors), the metal holes focus the red beam onto the red color producing phosphor, blue beam on the blue producing one etc. When focused on to a different pixel, the red beam again focuses on to the red phosphor and so on. Now, unlike the beam penetration CRTs where the acceleration of the electron beam was being monitored, we now manipulate the intensity of the 3 beams simultaneously. If the red beam is made more intense, we get more of red color in the final combination etc. Since fine-tuning of the beam intensities is comparatively simple, we can get much more combination of colors than the beam penetration case. In fact, one can have a matrix of combinations to produce a wide variety of colors. The shadow mask CRT, though better than the beam penetration CRT in performance, is not without it's disadvantages. Since three beams are to be focused, the role of the "Shadow mask" becomes critical. If the focusing is not achieved properly, the results tend to be poor. Also, since instead of one pixel point in a monochrome CRT now each pixel is made up of 3 points (for 3 colors), the resolution
a) Describe construction of a typical cathode ray tube for monitor. [4]
2.2 The Cathode Ray Tube (CRT/Monitor)
One of the basic and commonly used display devices is Cathode Ray Tube (CRT). A cathode ray tube is based on the simple concept that an electronic beam, when hits a phosphorescent surface, produces a beam of light
(momentarily - though we later describe surfaces that produce light intensities lashing over a period of time). Further, the beam of light itself can be focused to
any point on the screen by using suitable electronic / magnetic fields. The direction and intensity of the fields will allow one to determine the extent of the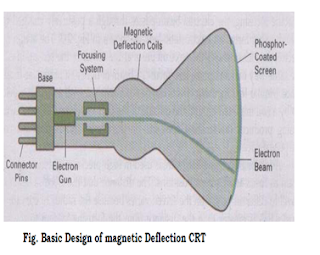
defection of the beam. Further these electronic / magnetic fields can be easily manipulated by using suitable electric fields with this background. In following section we describe the structure and working of the simple CRT.
Simple CRT makes use of a conical glass tube. At the narrow end of the glass tube an electronic gun is kept. This gun generates electrons that will be made to pass through the magnetic system called yoke. This magnetic
system is used for making the electronic beam to fall throughout the broad surface of the glass tube. The broad surface of the glass tube contains a single coat of high quality phosphorus. This reflects the electronic beam makes it to fall on the computer screen.
A pair of focusing grids - one horizontal and another vertical does the actual focusing of the electronic beam on to the screen. Electronic or magnetic fields operate these grids. Depending on the direction (positive or negative) and the intensity of the fields applied to them, the beam is deflected horizontally (or vertically) and thus, by using a suitable combination of these focusing grids; the beam can be focused to any point on the screen.
So, we now have a mechanism wherein any point on the screen can be illuminated (or made dark by simply switching off the beam). Hence, from a graphics point of view, any picture can be traced on the screen by the electron beam by suitably and continuously
manipulating the focusing grids and we get to see the picture on the screen "A basic graphic picture" of course, since the picture produced vanishes once the
beam is removed, to give the effect to continuity, we have to keep the beam retracing the picture continuously - (Refreshing).
Explain what is interlacing? [4]
Interlace is a technique of improving the picture quality of a video signal without consuming extra bandwidth. Interlaced video was designed for display on CRT televisions.
Interlaced scan refers to one of two common methods for "painting" a video image on an electronic display screen (the other being progressive scan) by scanning or displaying each line or row of pixels. This technique uses two fields to create a frame. One field contains all the odd lines in the image, the other contains all the even lines of the image. A PAL based television display, for example, scans 50 fields every second (25 odd and 25 even). The two sets of 25 fields work together to create a full frame every 1/25th of a second, resulting in a display of 25 frames per second.
To display interlaced video on modern progressive scan displays, a complex process called deinterlacing should be applied to the video signal or video data stored on a media.
a) What are frame buffers? What are its applications? [4]
e) Differentiate between the two graphics standard GKS and PHIGS. [4]
GKS is Graphical Kernel System. American National Standard ANSI X3.128-1985, which standardizes basic graphics functionality, and PHIGS (Programmer's Hierarchical Interactive Graphics System) is an API standard for rendering 3D computer graphics.
GKS (Graphics Kernel System) is an international standard for the functional interface to 2D graphics, whilst PHIGS (Progammer's Hierarchical Interactive Graphics System) is currently an ISO work item for 2D and 3D graphics. The Graphical Kernel System (GKS) was the first ISO standard for low-level computer graphics, introduced in 1977. GKS provides a set of drawing features for two-dimensional vector graphics suitable for charting and similar duties. PHIGS (Programmer's Hierarchical Interactive Graphics System) is an API standard for rendering 3D computer graphics, at one time considered to be the 3D graphics standard for the 1990s.
2. Transformation and Projections
b) What are oblique projections? [4]
oblique projections illustrate the general 3 dimensional shape of the object. However only faces of the object parallel to the plane of projection are shown at there true size and shape, that is angles and lengths are preserved for these faces only. In fact ,the oblique projection of these faces is equivalent to an orthographic front view.
TYPES OF OBLIQUE PROJECTIONS-
1.Cavalier 2.Cabinet
Cavalier Projection-A cavalier projection is obtained when the angle between oblique projectors and the plane of projection is 45 degree. In a cavalier projection the foreshortening factors for all three principal direction are equal. The resulting figure appears too thick. A cabinet projection is used to correct this deficiency.
Cabinet projection- An oblique projection for which the foreshortening factor for edges perpendicular to the plane of projection is one half is called a cabinet projection.
What do understand by the term 3-point perspective projection? Explain with the help of a diagram. [5]
Perspective (from Latin perspicere, to see through) in the graphic arts, such as drawing, is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are drawn:
• Smaller as their distance from the observer increases
• Foreshortened: the size of an object's dimensions along the line of sight are relatively shorter than dimensions across the line of sight (see later).
• Of the many types of perspective drawings, the most common categorizations of artificial perspective are one-, two- and three-point. The names of these categories refer to the number of vanishing points in the perspective drawing.
• One-point perspective
• One vanishing point is typically used for roads, railway tracks, hallways, or buildings viewed so that the front is directly facing the viewer. Any objects that are made up of lines either directly parallel with the viewer's line of sight or directly perpendicular (the railroad slats) can be represented with one-point perspective.
• One-point perspective exists when the painting plate (also known as the picture plane) is parallel to two axes of a rectilinear (or Cartesian) scene — a scene which is composed entirely of linear elements that intersect only at right angles. If one axis is parallel with the picture plane, then all elements are either parallel to the painting plate (either horizontally or vertically) or perpendicular to it. All elements that are parallel to the painting plate are drawn as parallel lines. All elements that are perpendicular to the painting plate converge at a single point (a vanishing point) on the horizon.
•
•
• Two-point perspective
• Walls in 2-pt perspective.
Walls converge towards 2 vanishing points.
All vertical beams are parallel.
Model by "The Great One" from 3D Warehouse.
Rendered in SketchUp.
• Two-point perspective can be used to draw the same objects as one-point perspective, rotated: looking at the corner of a house, or looking at two forked roads shrink into the distance, for example. One point represents one set of parallel lines, the other point represents the other. Looking at a house from the corner, one wall would recede towards one vanishing point, the other wall would recede towards the opposite vanishing point.
• Two-point perspective exists when the painting plate is parallel to a Cartesian scene in one axis (usually the z-axis) but not to the other two axes. If the scene being viewed consists solely of a cylinder sitting on a horizontal plane, no difference exists in the image of the cylinder between a one-point and two-point perspective.
• Two-point perspective has one set of lines parallel to the picture plane and two sets oblique to it.Parallel lines oblique to the picture plane converge to a vanishing point,which means that this set-up will require two vanishing points.
• Three-point perspective
•
Three-point perspective rendered from computer model by "Noel" from Google 3D Warehouse.
Rendered using IRender nXt.
• Three-point perspective is usually used for buildings seen from above (or below). In addition to the two vanishing points from before, one for each wall, there is now one for how those walls recede into the ground. This third vanishing point will be below the ground. Looking up at a tall building is another common example of the third vanishing point. This time the third vanishing point is high in space.
• Three-point perspective exists when the perspective is a view of a Cartesian scene where the picture plane is not parallel to any of the scene's three axes. Each of the three vanishing points corresponds with one of the three axes of the scene. Image constructed using multiple vanishing points.
• One-point, two-point, and three-point perspectives appear to embody different forms of calculated perspective. The methods required to generate these perspectives by hand are different. Mathematically, however, all three are identical: The difference is simply in the relative orientation of the rectilinear scene to the viewer.
• [edit] Four-point perspective
• Four point perspective, also called infinite-point perspective, is the curvilinear variant of two-point perspective. As the result when made into an infinite point version (i.e. when the amount of vanishing points exceeds the minimum amount required), a four point perspective image becomes a panorama that can go to a 360 degree view and beyond - when going beyond the 360 degree view the artist might depict an "impossible" room as the artist might depict something new when it's supposed to show part of what already exists within those 360 degrees. This elongated frame can be used both horizontally and vertically and when used vertically can be described as an image that depicts both a worms and birds eye view of a scene at the same time.
• As all other foreshortened variants of perspective (respectively one- to six-point perspective), it starts off with a horizon line, followed by four equally spaced vanishing points to delineate four vertical lines created in a 90 degree relation to the horizon line.
• The vanishing points made to create the curvilinear orthogonals are thus made ad hoc on the four vertical lines placed on the opposite side of the horizon line. The only dimension not foreshortened in this type of perspective being the rectilinear and parallell lines at a 90 degree angle to the horizon line - similar to the vertical lines used in two-point perspective.
• [edit] Zero-point perspective
• Because vanishing points exist only when parallel lines are present in the scene, a perspective without any vanishing points ("zero-point" perspective) occurs if the viewer is observing a nonlinear scene. The most common example of a nonlinear scene is a natural scene (e.g., a mountain range) which frequently does not contain any parallel lines. A perspective without vanishing points can still create a sense of "depth," as is clearly apparent in a photograph of a mountain range (more distant mountains have smaller scale features).
1. d) Explain one vanishing point projection from a point on z-axis. [4]
A vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used. The concept was first used by Renaissance artists such as Donatello, Masaccio and Leonardo da Vinci.
linear perspective is a drawing with 1-3 vanishing points.
curvilinear perspective is a drawing with either 4 or 5 vanishing points, in 5 point perspective the vanishing points are mapped into a circle with 4 vanishing points at the cardinal headings N,W,S,E and one at the circle origin.
reverse perspective is a drawing with vanishing points that are placed outside the painting with the illusion that they are "in front of" the painting.
Vanishing points can also refer to the point in the distance where the two verges of a road appear to converge. This is often used to help assess the upcoming curves in the road; to judge the radius and therefore the entry speed and optimum line. If the vanishing point moves towards you or to your sides, the curve is tightening. If the vanishing point moves away from you or comes to center, the curve is straightening
Vanishing Points
Any set of parallel lines that are not parallel to the projection plane will converge to a vanishing point.If the set of lines is parallel to one of the three principal axis then it is called a principal vanishing point.
In this image the X and Y lines are parallel to the Z axis. Since the projection plane is normal to the Z axis there is only one principal vanishing point. Lines parallel to either X or Y axis are parallel to projection planeand have no vanishing point. So it is a one-point projection.
In this image the lines are not parallel to the z axis. Since the projection plane is normal to the z axis there is only one principal vanishing point. Lines parallel to either x or y axis are parallel to projection planeand have no vanishing point. So it is a one-point projection.
b) How are points at Infinity represented In homogenous coordinate system? [4]
Ideal Points or Points at Infinity
As mentioned at the very beginning of this page, homogeneous coordinates can easily capture the concept of infinity. Let a point (x,y) be fixed and converted to a homogeneous coordinate by multiplying with 1/w, (x/w,y/w,1/w). Let the value of w approach to zero, then (x/w,y/w) moves farther and farther away in the direction of (x,y). When w becomes zero, (x/w,y/w) moves to infinity. Therefore, we would say, the homogeneous coordinate (x,y,0) is the ideal point or point at infinity in the direction of (x,y).
Let us take a look at an example. Let (3,5) be a point in the xy-plane. Consider (3/w,5/w). If w is not zero, this point lies on the line y = (5/3) x. Or, if you like the vector form, (3/w,5/w) is a point on the line O + (1/w)d, where the base point O is the coordinate origin and d is the direction vector <3>. Therefore, as w approaches zero, the point moves to infinity on the line. This is why we say (x,y,0) is the ideal point or the point at infinity in the direction of (x,y).
The story is the same for points in space, where (x,y,z,0) is the ideal point or point at infinity in the direction of (x,y,z).
The concept of homogeneous coordinates and points at infinity in certain direction will become very important when we discuss representations of curves and surface.
Differentiate between parallel, perspective and isometric projection and their uses. [7]
ISOMETRIC PROJECTION Isometric projection is the most frequently used type of axonometric projection, which is a method used to show an object in all three dimensions in a single view. Axonometric projection is a form of orthographic projection in which the projectors are always perpendicular to the plane of projection. However, the object itself, rather than the projectors, are at an angle to the plane of projection. Figure 3-6 shows a cube projected by isometric projection. The cube is angled so that all of its surfaces make the same angle with the plane of projection. As a result, the length of each of the edges shown in the projection is somewhat shorter than the actual length of the edge on the object itself. This reduction is called foreshortening. Since all of the surfaces make the angle with the plane of projection, the edges foreshorten in the same ratio. Therefore, one scale can be used for the entire layout; hence, the term isometric which literally means the same scale. VIEWS The following pages will help you understand the types of views commonly used in blueprints. MULTIVIEW DRAWINGS The complexity of the shape of a drawing governs the number of views needed to project the drawing. Complex drawings normally have six views: both ends, front, top, rear, and bottom. However, most drawings are less complex and are shown in three views.
This is simply a way of projecting the third dimension from a flat 2 dimensional drawing - easy enough to do with simple shapes but not very convincing where other shapes are concerned. It varies from true perspective in that the lines don't converge at vanishing points.
Isometric projection is a form of graphical projection — more specifically, an axonometric projection. It is a method of visually representing three-dimensional objects in two dimensions, in which the three coordinate axes appear equally foreshortened and the angles between any two of them are 120°. Isometric projection is one of the projections used in drafting engineering drawings.
The term isometric comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (this is not true of some other forms of graphical projection).
One of the advantages of isometric perspective in engineering drawings is that 60° angles are easy to construct using only a compass and straightedge.
You can create realistic visual effects in a drawing by defining either parallel or perspective projections of a model.
The difference between perspective views and parallel projections is that perspective views require a distance between a theoretical camera and target point. Small distances produce severe perspective effects; large distances produce mild effects.
Parallel Projection
Parallel projection is just a cheap imitation of what the real world would look like. This is because it simply ignores the z extent of all points. It is just concerned with the easiest way of getting the point to the screen. For these reasons, parallel projection is very easy to do and is good for modeling where perspective would distort construction, but it is not used as much as perspective projection. For the rest of this tutorial, assume that we are dealing with members of our point class that we developed. Notice that our test object to the right after projection each edge is perfectly aligned just as it was in the world. Each edge that was parallel in the world appears parallel in the projection. The transition from world coordinates to screen coordinates is very simple.
sx = wx+XCenter
sy = -wy+YCenter
Remember that our world is designed to be viewed from the center (0,0,0). If we just used the world coordinates, our view would be incorrect! This is because the upper left of the screen is (0,0) and this is NOT aigned with what we want. To correct this, we must add half the screen width and half the screen height to our world coordinates so that the views are the same. Also notice that we are taking -1*wy. By now you should be able to guess why! It is because in our world, as the object moves up, its y extent increases. This is completely opposite of our screen where moving down increases its y extent. Multiplying the y extent by -1 will correct this problem as well! I told you it was simple!
Perspective Projection
This type of projection is a little more complicted than parallel projection, but the results are well worth it. We are able to realistically display our world as if we were really standing there looking around! The same display issues face us as before
1. We need to align the screen (0,0) with the world (0,0,0)
2. We need to correct the y directional error.
We correct the two problems as we did before. We add half the screen width and height to our point, and then reverse the sign of the y extent. Here's a generalized equation for the actual perspective projection.
OneOverZ= 1/wz;
sx = wx * XSCALE * OneOverZ + XCenter;
sy = -wy * YSCALE * OneOverZ + YCenter;
sz = wz;
a) Explain the difference between orthographic projection and isometric projection with the help of diagrams. Indicate their applications. [6+3]
Orthographic projection is the arrangement of Plan, Side, Font or Back elevations on a 2 dimensional drawing. It shouldn't be confused with axonometric, which is a sketch with lines at 45 degrees to simulate a 3D view.
Isometric is a drawing method where horizontal lines are drawn at 30 degree instead, whilst vertical lines are always vertical. There is no vanishing point.
Orthographic projections are drawn to a vanishing point while Isometric projections are not and are also based on a 3 120 degree axis.
b) What are advantages and disadvantages of homogenous co-ordinates? [4]
hey have the advantage that the coordinates of a point, even those at infinity, can be represented using finite coordinates. Often formulas involving homogeneous coordinates are simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.
If the homogeneous coordinates of a point are multiplied by a non-zero scalar then the resulting coordinates represent the same point. An additional condition must be added on the coordinates to ensure that only one set of coordinates corresponds to a given point, so the number of coordinates required is, in general, one more than the dimension of the projective space being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates are required to specify a point on the projective plane.






What is the relationship between the translations Ttx,ty , T -tx, -ty and (T tx , ty )-1? [4]
b) What is the relationship between the rotations Rθ , R-θ and Rθ-1. [4]
Translations and Rotations on the xy-Plane
We intend to translate a point in the xy-plane to a new place by adding a vector . It is not difficult to see that between a point (x, y) and its new place (x', y'), we have x' = x + h and y' = y + k. Let us use a form similar to the homogeneous coordinates. That is, a point becomes a column vector whose third component is 1. Thus, point (x,y) becomes the following:
Then, the relationship between (x, y) and (x', y') can be put into a matrix form like the following:
Therefore, if a line has an equation Ax + By + C = 0, after plugging the formulae for x and y, the line has a new equation Ax' + By' + (-Ah - Bk + C) = 0.
If a point (x, y) is rotated an angle a about the coordinate origin to become a new point (x', y'), the relationships can be described as follows:
Thus, rotating a line Ax + By + C = 0 about the origin a degree brings it to a new equation:
(Acosa - Bsina)x' + (Asina + Bcosa)y' + C = 0
Translations and rotations can be combined into a single equation like the following:
The above means that rotates the point (x,y) an angle a about the coordinate origin and translates the rotated result in the direction of (h,k). However, if translation (h,k) is applied first followed by a rotation of angle a (about the coordinate origin), we will have the following:
Therefore, rotation and translation are not commutative!
In the above discussion, we always present two matrices, A and B, one for transforming x to x' (i.e., x'=Ax) and the other for transforming x' to x (i.e., x=Bx'). You can verify that the product of A and B is the identity matrix. In other words, A and B are inverse matrices of each other. Therefore, if we know one of them, the other is the inverse of the given one. For example, if you know A that transforms x to x', the matrix that transforms x' back to x is the inverse of A.
Let R be a transformation matrix sending x' to x: x=Rx'. Plugging this equation of x into a conic equation gives the following:
Rearranging terms yields
This is the new equation of the given conic after the specified transformation. Note that the new 3-by-3 symmetric matrix that represents the conic in a new position is the following:
Now you see the power of matrices in describing the concept of transformation.
Translations and Rotations in Space
Translations in space is similar to the plane version:
The above translates points by adding a vector
Raster-scan system:-
1)raster displays have less resolution.
2)the lines produced are zig-zag as the plotted values are discrete.
3)high degree realism is achieved in picture with the aid of advanced shading and hidden surface technique.
4)decreasing memory costs have made raster systems popular.
Random scan system:-
1)random displays have high resolutions since the picture defination is stored as a set of line drawing commands and not as a set of intensity values.
2)smooth lines are produced as the electron beam directly follows the line path.
3)realism is difficult to achieve.
4)random-scan system's are generally costlier.
a) Explain why RGB color model is used for display. How different shades of colors are generated on the RGB monitors. [6]
The RGB color model creates colors by mixing light, red, green and blue. All video displays are RGB. Since it is impossible to print a light mixture printers are able to simulate full color by using four colors, cyan, magenta, yellow and black. Most new color laser copy machines automatically convert RGB to CMYK when a digital file is sent, but the results may be off color.
1. e) Explain how colour images are displayed on a computer monitor. [4]
2.3 CRTs for Color Display
This was one the earlier CRTs to produce color displays. Coating phosphors of different compounds can produce different colored pictures. But the basic problem of graphics is not to produce a picture of a predetermined color, but to produce color pictures, with the color characteristics chosen at run time. The basic principle behind colored displays is that combining the 3 basic colors –Red, Blue and Green, can produce every color. By choosing different ratios of these three colors we can produce different colors – millions of them in-fact. We also have basic phosphors, which can produce these basic colors. So, one should have a technology to combine them in different combinations.
2.4 Beam Penetration CRT
This CRT is similar to the simple CRT, but it makes use of multi coloured phosphorus of number of layers. Each phosphorus layer is responsible for one colour. All other arrangements are similar to simple CRT. It can produce a maximum of 4 to 5 colours The organization is something like this - The red, green and blue phosphorus are coated in layers - one behind the other. If a low speed beam strikes the CRT, only the red colored phosphorus is activated, a slightly accelerated beam would activate both red and green (because it can penetrate deeper) and a much more activated one would add the blue component also. But the basic problem is a reliable technology to accelerate the electronic beam to precise levels to get the exact colors - it is easier said than done. However, a limited range of colors can be conveniently produced using the concept.
c) Explain shadow masking method for colour monitor. [4]
The shadow mask CRT, instead of using one electron gun, uses 3 different guns placed one by the side of the other to form a triangle or a "Delta" as shown. Each pixel point on the screen is also made up of 3 types of phosphors to produce red, blue and green colors. Just before the phosphor screen is a metal screen, called a "shadow mask". This plate has holes placed strategically, so that when the beams from the three electron guns are focused on a particular pixel, they get focused on particular color producing pixel only i.e. If for convenience sake we can call the electronic beams as red, blue and
green beams (though in practice the colors are produced by the phosphors, and until the beams hit the phosphor dots, they produce no colors), the metal holes focus the red beam onto the red color producing phosphor, blue beam on the blue producing one etc. When focused on to a different pixel, the red beam again focuses on to the red phosphor and so on. Now, unlike the beam penetration CRTs where the acceleration of the electron beam was being monitored, we now manipulate the intensity of the 3 beams simultaneously. If the red beam is made more intense, we get more of red color in the final combination etc. Since fine-tuning of the beam intensities is comparatively simple, we can get much more combination of colors than the beam penetration case. In fact, one can have a matrix of combinations to produce a wide variety of colors. The shadow mask CRT, though better than the beam penetration CRT in performance, is not without it's disadvantages. Since three beams are to be focused, the role of the "Shadow mask" becomes critical. If the focusing is not achieved properly, the results tend to be poor. Also, since instead of one pixel point in a monochrome CRT now each pixel is made up of 3 points (for 3 colors), the resolution
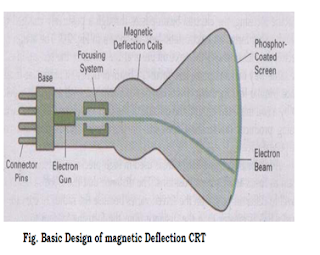
a) Describe construction of a typical cathode ray tube for monitor. [4]
2.2 The Cathode Ray Tube (CRT/Monitor)
One of the basic and commonly used display devices is Cathode Ray Tube (CRT). A cathode ray tube is based on the simple concept that an electronic beam, when hits a phosphorescent surface, produces a beam of light
(momentarily - though we later describe surfaces that produce light intensities lashing over a period of time). Further, the beam of light itself can be focused to
any point on the screen by using suitable electronic / magnetic fields. The direction and intensity of the fields will allow one to determine the extent of the

defection of the beam. Further these electronic / magnetic fields can be easily manipulated by using suitable electric fields with this background. In following section we describe the structure and working of the simple CRT.
Simple CRT makes use of a conical glass tube. At the narrow end of the glass tube an electronic gun is kept. This gun generates electrons that will be made to pass through the magnetic system called yoke. This magnetic
system is used for making the electronic beam to fall throughout the broad surface of the glass tube. The broad surface of the glass tube contains a single coat of high quality phosphorus. This reflects the electronic beam makes it to fall on the computer screen.
A pair of focusing grids - one horizontal and another vertical does the actual focusing of the electronic beam on to the screen. Electronic or magnetic fields operate these grids. Depending on the direction (positive or negative) and the intensity of the fields applied to them, the beam is deflected horizontally (or vertically) and thus, by using a suitable combination of these focusing grids; the beam can be focused to any point on the screen.
So, we now have a mechanism wherein any point on the screen can be illuminated (or made dark by simply switching off the beam). Hence, from a graphics point of view, any picture can be traced on the screen by the electron beam by suitably and continuously
manipulating the focusing grids and we get to see the picture on the screen "A basic graphic picture" of course, since the picture produced vanishes once the
beam is removed, to give the effect to continuity, we have to keep the beam retracing the picture continuously - (Refreshing).
Explain what is interlacing? [4]
Interlace is a technique of improving the picture quality of a video signal without consuming extra bandwidth. Interlaced video was designed for display on CRT televisions.
Interlaced scan refers to one of two common methods for "painting" a video image on an electronic display screen (the other being progressive scan) by scanning or displaying each line or row of pixels. This technique uses two fields to create a frame. One field contains all the odd lines in the image, the other contains all the even lines of the image. A PAL based television display, for example, scans 50 fields every second (25 odd and 25 even). The two sets of 25 fields work together to create a full frame every 1/25th of a second, resulting in a display of 25 frames per second.
To display interlaced video on modern progressive scan displays, a complex process called deinterlacing should be applied to the video signal or video data stored on a media.
a) What are frame buffers? What are its applications? [4]

e) Differentiate between the two graphics standard GKS and PHIGS. [4]
GKS is Graphical Kernel System. American National Standard ANSI X3.128-1985, which standardizes basic graphics functionality, and PHIGS (Programmer's Hierarchical Interactive Graphics System) is an API standard for rendering 3D computer graphics.
GKS (Graphics Kernel System) is an international standard for the functional interface to 2D graphics, whilst PHIGS (Progammer's Hierarchical Interactive Graphics System) is currently an ISO work item for 2D and 3D graphics. The Graphical Kernel System (GKS) was the first ISO standard for low-level computer graphics, introduced in 1977. GKS provides a set of drawing features for two-dimensional vector graphics suitable for charting and similar duties. PHIGS (Programmer's Hierarchical Interactive Graphics System) is an API standard for rendering 3D computer graphics, at one time considered to be the 3D graphics standard for the 1990s.
2. Transformation and Projections
b) What are oblique projections? [4]
oblique projections illustrate the general 3 dimensional shape of the object. However only faces of the object parallel to the plane of projection are shown at there true size and shape, that is angles and lengths are preserved for these faces only. In fact ,the oblique projection of these faces is equivalent to an orthographic front view.
TYPES OF OBLIQUE PROJECTIONS-
1.Cavalier 2.Cabinet
Cavalier Projection-A cavalier projection is obtained when the angle between oblique projectors and the plane of projection is 45 degree. In a cavalier projection the foreshortening factors for all three principal direction are equal. The resulting figure appears too thick. A cabinet projection is used to correct this deficiency.
Cabinet projection- An oblique projection for which the foreshortening factor for edges perpendicular to the plane of projection is one half is called a cabinet projection.
What do understand by the term 3-point perspective projection? Explain with the help of a diagram. [5]
Perspective (from Latin perspicere, to see through) in the graphic arts, such as drawing, is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are drawn:
• Smaller as their distance from the observer increases
• Foreshortened: the size of an object's dimensions along the line of sight are relatively shorter than dimensions across the line of sight (see later).
• Of the many types of perspective drawings, the most common categorizations of artificial perspective are one-, two- and three-point. The names of these categories refer to the number of vanishing points in the perspective drawing.
• One-point perspective
• One vanishing point is typically used for roads, railway tracks, hallways, or buildings viewed so that the front is directly facing the viewer. Any objects that are made up of lines either directly parallel with the viewer's line of sight or directly perpendicular (the railroad slats) can be represented with one-point perspective.
• One-point perspective exists when the painting plate (also known as the picture plane) is parallel to two axes of a rectilinear (or Cartesian) scene — a scene which is composed entirely of linear elements that intersect only at right angles. If one axis is parallel with the picture plane, then all elements are either parallel to the painting plate (either horizontally or vertically) or perpendicular to it. All elements that are parallel to the painting plate are drawn as parallel lines. All elements that are perpendicular to the painting plate converge at a single point (a vanishing point) on the horizon.
•

•
• Two-point perspective
• Walls in 2-pt perspective.
Walls converge towards 2 vanishing points.
All vertical beams are parallel.
Model by "The Great One" from 3D Warehouse.
Rendered in SketchUp.
• Two-point perspective can be used to draw the same objects as one-point perspective, rotated: looking at the corner of a house, or looking at two forked roads shrink into the distance, for example. One point represents one set of parallel lines, the other point represents the other. Looking at a house from the corner, one wall would recede towards one vanishing point, the other wall would recede towards the opposite vanishing point.
• Two-point perspective exists when the painting plate is parallel to a Cartesian scene in one axis (usually the z-axis) but not to the other two axes. If the scene being viewed consists solely of a cylinder sitting on a horizontal plane, no difference exists in the image of the cylinder between a one-point and two-point perspective.
• Two-point perspective has one set of lines parallel to the picture plane and two sets oblique to it.Parallel lines oblique to the picture plane converge to a vanishing point,which means that this set-up will require two vanishing points.
• Three-point perspective
•
Three-point perspective rendered from computer model by "Noel" from Google 3D Warehouse.
Rendered using IRender nXt.
• Three-point perspective is usually used for buildings seen from above (or below). In addition to the two vanishing points from before, one for each wall, there is now one for how those walls recede into the ground. This third vanishing point will be below the ground. Looking up at a tall building is another common example of the third vanishing point. This time the third vanishing point is high in space.
• Three-point perspective exists when the perspective is a view of a Cartesian scene where the picture plane is not parallel to any of the scene's three axes. Each of the three vanishing points corresponds with one of the three axes of the scene. Image constructed using multiple vanishing points.
• One-point, two-point, and three-point perspectives appear to embody different forms of calculated perspective. The methods required to generate these perspectives by hand are different. Mathematically, however, all three are identical: The difference is simply in the relative orientation of the rectilinear scene to the viewer.
• [edit] Four-point perspective
• Four point perspective, also called infinite-point perspective, is the curvilinear variant of two-point perspective. As the result when made into an infinite point version (i.e. when the amount of vanishing points exceeds the minimum amount required), a four point perspective image becomes a panorama that can go to a 360 degree view and beyond - when going beyond the 360 degree view the artist might depict an "impossible" room as the artist might depict something new when it's supposed to show part of what already exists within those 360 degrees. This elongated frame can be used both horizontally and vertically and when used vertically can be described as an image that depicts both a worms and birds eye view of a scene at the same time.
• As all other foreshortened variants of perspective (respectively one- to six-point perspective), it starts off with a horizon line, followed by four equally spaced vanishing points to delineate four vertical lines created in a 90 degree relation to the horizon line.
• The vanishing points made to create the curvilinear orthogonals are thus made ad hoc on the four vertical lines placed on the opposite side of the horizon line. The only dimension not foreshortened in this type of perspective being the rectilinear and parallell lines at a 90 degree angle to the horizon line - similar to the vertical lines used in two-point perspective.
• [edit] Zero-point perspective
• Because vanishing points exist only when parallel lines are present in the scene, a perspective without any vanishing points ("zero-point" perspective) occurs if the viewer is observing a nonlinear scene. The most common example of a nonlinear scene is a natural scene (e.g., a mountain range) which frequently does not contain any parallel lines. A perspective without vanishing points can still create a sense of "depth," as is clearly apparent in a photograph of a mountain range (more distant mountains have smaller scale features).
1. d) Explain one vanishing point projection from a point on z-axis. [4]
A vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used. The concept was first used by Renaissance artists such as Donatello, Masaccio and Leonardo da Vinci.
linear perspective is a drawing with 1-3 vanishing points.
curvilinear perspective is a drawing with either 4 or 5 vanishing points, in 5 point perspective the vanishing points are mapped into a circle with 4 vanishing points at the cardinal headings N,W,S,E and one at the circle origin.
reverse perspective is a drawing with vanishing points that are placed outside the painting with the illusion that they are "in front of" the painting.
Vanishing points can also refer to the point in the distance where the two verges of a road appear to converge. This is often used to help assess the upcoming curves in the road; to judge the radius and therefore the entry speed and optimum line. If the vanishing point moves towards you or to your sides, the curve is tightening. If the vanishing point moves away from you or comes to center, the curve is straightening
Vanishing Points
Any set of parallel lines that are not parallel to the projection plane will converge to a vanishing point.If the set of lines is parallel to one of the three principal axis then it is called a principal vanishing point.
In this image the X and Y lines are parallel to the Z axis. Since the projection plane is normal to the Z axis there is only one principal vanishing point. Lines parallel to either X or Y axis are parallel to projection planeand have no vanishing point. So it is a one-point projection.

In this image the lines are not parallel to the z axis. Since the projection plane is normal to the z axis there is only one principal vanishing point. Lines parallel to either x or y axis are parallel to projection planeand have no vanishing point. So it is a one-point projection.
b) How are points at Infinity represented In homogenous coordinate system? [4]
Ideal Points or Points at Infinity
As mentioned at the very beginning of this page, homogeneous coordinates can easily capture the concept of infinity. Let a point (x,y) be fixed and converted to a homogeneous coordinate by multiplying with 1/w, (x/w,y/w,1/w). Let the value of w approach to zero, then (x/w,y/w) moves farther and farther away in the direction of (x,y). When w becomes zero, (x/w,y/w) moves to infinity. Therefore, we would say, the homogeneous coordinate (x,y,0) is the ideal point or point at infinity in the direction of (x,y).
Let us take a look at an example. Let (3,5) be a point in the xy-plane. Consider (3/w,5/w). If w is not zero, this point lies on the line y = (5/3) x. Or, if you like the vector form, (3/w,5/w) is a point on the line O + (1/w)d, where the base point O is the coordinate origin and d is the direction vector <3>. Therefore, as w approaches zero, the point moves to infinity on the line. This is why we say (x,y,0) is the ideal point or the point at infinity in the direction of (x,y).
The story is the same for points in space, where (x,y,z,0) is the ideal point or point at infinity in the direction of (x,y,z).
The concept of homogeneous coordinates and points at infinity in certain direction will become very important when we discuss representations of curves and surface.
Differentiate between parallel, perspective and isometric projection and their uses. [7]
ISOMETRIC PROJECTION Isometric projection is the most frequently used type of axonometric projection, which is a method used to show an object in all three dimensions in a single view. Axonometric projection is a form of orthographic projection in which the projectors are always perpendicular to the plane of projection. However, the object itself, rather than the projectors, are at an angle to the plane of projection. Figure 3-6 shows a cube projected by isometric projection. The cube is angled so that all of its surfaces make the same angle with the plane of projection. As a result, the length of each of the edges shown in the projection is somewhat shorter than the actual length of the edge on the object itself. This reduction is called foreshortening. Since all of the surfaces make the angle with the plane of projection, the edges foreshorten in the same ratio. Therefore, one scale can be used for the entire layout; hence, the term isometric which literally means the same scale. VIEWS The following pages will help you understand the types of views commonly used in blueprints. MULTIVIEW DRAWINGS The complexity of the shape of a drawing governs the number of views needed to project the drawing. Complex drawings normally have six views: both ends, front, top, rear, and bottom. However, most drawings are less complex and are shown in three views.
This is simply a way of projecting the third dimension from a flat 2 dimensional drawing - easy enough to do with simple shapes but not very convincing where other shapes are concerned. It varies from true perspective in that the lines don't converge at vanishing points.
Isometric projection is a form of graphical projection — more specifically, an axonometric projection. It is a method of visually representing three-dimensional objects in two dimensions, in which the three coordinate axes appear equally foreshortened and the angles between any two of them are 120°. Isometric projection is one of the projections used in drafting engineering drawings.
The term isometric comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (this is not true of some other forms of graphical projection).
One of the advantages of isometric perspective in engineering drawings is that 60° angles are easy to construct using only a compass and straightedge.
You can create realistic visual effects in a drawing by defining either parallel or perspective projections of a model.
The difference between perspective views and parallel projections is that perspective views require a distance between a theoretical camera and target point. Small distances produce severe perspective effects; large distances produce mild effects.
Parallel Projection
Parallel projection is just a cheap imitation of what the real world would look like. This is because it simply ignores the z extent of all points. It is just concerned with the easiest way of getting the point to the screen. For these reasons, parallel projection is very easy to do and is good for modeling where perspective would distort construction, but it is not used as much as perspective projection. For the rest of this tutorial, assume that we are dealing with members of our point class that we developed. Notice that our test object to the right after projection each edge is perfectly aligned just as it was in the world. Each edge that was parallel in the world appears parallel in the projection. The transition from world coordinates to screen coordinates is very simple.
sx = wx+XCenter
sy = -wy+YCenter
Remember that our world is designed to be viewed from the center (0,0,0). If we just used the world coordinates, our view would be incorrect! This is because the upper left of the screen is (0,0) and this is NOT aigned with what we want. To correct this, we must add half the screen width and half the screen height to our world coordinates so that the views are the same. Also notice that we are taking -1*wy. By now you should be able to guess why! It is because in our world, as the object moves up, its y extent increases. This is completely opposite of our screen where moving down increases its y extent. Multiplying the y extent by -1 will correct this problem as well! I told you it was simple!
Perspective Projection
This type of projection is a little more complicted than parallel projection, but the results are well worth it. We are able to realistically display our world as if we were really standing there looking around! The same display issues face us as before
1. We need to align the screen (0,0) with the world (0,0,0)
2. We need to correct the y directional error.
We correct the two problems as we did before. We add half the screen width and height to our point, and then reverse the sign of the y extent. Here's a generalized equation for the actual perspective projection.
OneOverZ= 1/wz;
sx = wx * XSCALE * OneOverZ + XCenter;
sy = -wy * YSCALE * OneOverZ + YCenter;
sz = wz;
a) Explain the difference between orthographic projection and isometric projection with the help of diagrams. Indicate their applications. [6+3]
Orthographic projection is the arrangement of Plan, Side, Font or Back elevations on a 2 dimensional drawing. It shouldn't be confused with axonometric, which is a sketch with lines at 45 degrees to simulate a 3D view.
Isometric is a drawing method where horizontal lines are drawn at 30 degree instead, whilst vertical lines are always vertical. There is no vanishing point.
Orthographic projections are drawn to a vanishing point while Isometric projections are not and are also based on a 3 120 degree axis.
b) What are advantages and disadvantages of homogenous co-ordinates? [4]
hey have the advantage that the coordinates of a point, even those at infinity, can be represented using finite coordinates. Often formulas involving homogeneous coordinates are simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.
If the homogeneous coordinates of a point are multiplied by a non-zero scalar then the resulting coordinates represent the same point. An additional condition must be added on the coordinates to ensure that only one set of coordinates corresponds to a given point, so the number of coordinates required is, in general, one more than the dimension of the projective space being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates are required to specify a point on the projective plane.







What is the relationship between the translations Ttx,ty , T -tx, -ty and (T tx , ty )-1? [4]
b) What is the relationship between the rotations Rθ , R-θ and Rθ-1. [4]
Translations and Rotations on the xy-Plane
We intend to translate a point in the xy-plane to a new place by adding a vector
Then, the relationship between (x, y) and (x', y') can be put into a matrix form like the following:
Therefore, if a line has an equation Ax + By + C = 0, after plugging the formulae for x and y, the line has a new equation Ax' + By' + (-Ah - Bk + C) = 0.
If a point (x, y) is rotated an angle a about the coordinate origin to become a new point (x', y'), the relationships can be described as follows:
Thus, rotating a line Ax + By + C = 0 about the origin a degree brings it to a new equation:
(Acosa - Bsina)x' + (Asina + Bcosa)y' + C = 0
Translations and rotations can be combined into a single equation like the following:
The above means that rotates the point (x,y) an angle a about the coordinate origin and translates the rotated result in the direction of (h,k). However, if translation (h,k) is applied first followed by a rotation of angle a (about the coordinate origin), we will have the following:
Therefore, rotation and translation are not commutative!
In the above discussion, we always present two matrices, A and B, one for transforming x to x' (i.e., x'=Ax) and the other for transforming x' to x (i.e., x=Bx'). You can verify that the product of A and B is the identity matrix. In other words, A and B are inverse matrices of each other. Therefore, if we know one of them, the other is the inverse of the given one. For example, if you know A that transforms x to x', the matrix that transforms x' back to x is the inverse of A.
Let R be a transformation matrix sending x' to x: x=Rx'. Plugging this equation of x into a conic equation gives the following:
Rearranging terms yields
This is the new equation of the given conic after the specified transformation. Note that the new 3-by-3 symmetric matrix that represents the conic in a new position is the following:
Now you see the power of matrices in describing the concept of transformation.
Translations and Rotations in Space
Translations in space is similar to the plane version:
The above translates points by adding a vector
.
Rotations in space are more complex, because we can either rotate about the x-axis, the y-axis or the z-axis. When rotating about the z-axis, only coordinates of x and y will change and the z-coordinate will be the same. In effect, it is exactly a rotation about the origin in the xy-plane. Therefore, the rotation equation is
With this set of equations, letting a be 90 degree rotates (1,0,0) to (0,1,0) and (0,1,0) to (-1,0,0). Therefore, the x-axis rotates to the y-axis and the y-axis rotates to the negative direction of the original x-axis. This is the effect of rotating about the z-axis 90 degree.
Based on the same idea, rotating about the x-axis an angle a is the following:
Let us verify the above again with a being 90 degree. This rotates (0,1,0) to (0,0,1) and (0,0,1) to (0,-1,0). Thus, the y-axis rotates to the z-axis and the z-axis rotates to the negative direction of the original y-axis.
But, rotating about the y-axis is different! It is because the way of measuring angles. In a right-handed system, if your right hand holds a coordinate axis with your thumb pointing in the positive direction, your other four fingers give the positive direction of angle measuring. More precisely, the positive direction for measuring angles is from the z-axis to x-axis. However, traditionally the angle measure is from the x-axis to the z-axis. As a result, rotating an angle a about the y-axis in the sense of a right-handed system is equivalent to rotating an angle -a measuring from the x-axis to the z-axis. Therefore, the rotation equations are
Let us verify the above with rotating about the y-axis 90 degree. This rotates (1,0,0) to (0,0,-1) and (0,0,1) to (1,0,0). Therefore, the x-axis rotates to the negative direction of the z-axis and the z-axis rotates to the original x-axis.
A rotation matrix and a translation matrix can be combined into a single matrix as follows, where the r's in the upper-left 3-by-3 matrix form a rotation and p, q and r form a translation vector. This matrix represents rotations followed by a translation.
You can apply this transformation to a plane and a quadric surface just as what we did for lines and conics earlier.
b) Describe the Sutherland-Cohen algorithm for clipping? Is this applicable to any type of window? Justify your answer. [9]
The Cohen-Sutherland Line-Clipping Algorithm
The more efficient Cohen-Sutherland Algorithm performs initial tests on a line to determine whether intersection calculations can be avoided.
Steps for Cohen-Sutherland algorithm
1. End-points pairs are check for trivial acceptance or trivial rejected using the outcode.
2. If not trivial-accepance or trivial-rejected, divided into two segments at a clip edge.
3. Iteratively clipped by testing trivial-acceptance or trivial-rejected, and divided into two segments until completely inside or trivial-rejected.
Pseudo-code of Cohen-Sutherland Algorithm.
Trivial acceptance/reject test
To perform trivial accept and reject tests, we extend the edges of the clip rectangle to divide the plane of the clip rectangle into nine regions. Each region is assigned a 4-bit code deteermined by where the region lies with respect to the outside halfplanes of the clip-rectangle edges. Each bit in the outcode is set to either 1 (true) or 0 (false); the 4 bits in the code correspond to the following conditions:
o Bit 1 : outside halfplane of top edge, above top edge
Y > Ymax
o Bit 2 : outside halfplane of bottom edge, below bottom edge
Y < Ymin
o Bit 3 : outside halfplane of right edge, to the right of right edge
X > Xmax
o Bit 4 : outside halfplane of left edge, to the left of left edge
X < Xmin
Conclusion
In summary, the C-S algorithm is efficient when outcode testing can be done cheaply (for example, by doing bitwise operations in assembly language) and trivial acceptance or rejection is applicable to the majority of line segments .(For example, large windows - everything is inside , or small windows - everything is outside).
3.b) Explain the steps of the Cyrus-Beck line-clipping algorithm. [6]
The Cyrus–Beck algorithm is a line clipping algorithm. It was designed to be more efficient than the Sutherland–Cohen algorithm which uses repetitive clipping [1]. Cyrus–Beck is a general algorithm and can be used with a convex polygon clipping window unlike Sutherland-Cohen that can be used only on a rectangular clipping area
Here the parametric equation of a line in the view plane is:
P(t) = P(0) + t(P1 − P0)
where t = 0 at P(1) t = o at t0
Now to find intersection point with the clipping window we calculate value of dot product
n(Pt-f)
{if > 0 vector pointed toward interior
if = 0 vector pointed parallel to plane containing f
if < 0 vector pointed away from interior
here n stands for normal.
By this we select the point of intersection of line and clipping window where (dot product = 0 ) and hence clip the line
c) Why clipping Is an Important operation for rendering? [4]
b) Is it necessary to compute lighting information before clipping for rendering a 3D scene? Explain. [6]
Geometry in the complete 3D scene is lit according to the defined locations of light sources and reflectance and other surface properties. Current hardware implementations of the graphics pipeline compute lighting only at the vertices of the polygons being rendered. The lighting values between vertices are then interpolated during rasterization. Per-fragment (i.e. per-pixel) lighting can be done on modern graphics hardware as a post-rasterization process by means of a shader program.
.Outline the steps required to generate a hidden-surface image using the depth-buffer approach and then comment on the relative merits of this approach compared with the scan-line algorithm. [18]
Comparison of Visibility Algorithms
ray casting:
memory: used for object database
implementation: easy, but to make it fast you need spatial data structures
speed: slow if many objects: cost is O((#pixels)´(#objects))
generality: excellent, can even do CSG (constructive solid geometry), shadows, transp.
painter’s:
memory: used for image buffer
implementation: moderate, requires scan conversion; hard if sorting & splitting needed
speed: fast if objects can be sorted a priori, otherwise sorting many objs. can be costly
generality: splitting of intersecting objects & sorting make it clumsy for general 3-D rendering
z-buffer:
memory: used for image buffer & z-buffer
implementation: moderate, requires scan conversion. It can be put in hardware.
speed: fast, unless depth complexity is high (redundant shading)
generality: very good
others (scanline, object space): tend to be hard to implement, and very hard to generalize to non-polygon models
c) Describe the features of Depths sort algorithm. [6]
It is one solution to the visibility problem, which is the problem of deciding which elements of a rendered scene are visible, and which are hidden. The painter's algorithm is another common solution which, though less efficient, can also handle non-opaque scene elements. Z-buffering is also known as depth buffering.
Algorithm:
• Sort the polygons in the scene by their depth
• Draw them back to front
• Problem: Unless all polygons have constant z, a strict depth ordering may not exist
Note: Constant z case is important in VLSI design
Depth Sort (Painter Algorithm)
• General Case: Given two polygons P and Q, an order may be determined between them, if at least
one of the following holds:
1) z values of P and Q do not overlap 2) The bounding rectangle in the x, y plane for P and Q do not overlap
3) P is totally on one side of Q’s plane 4) Q is totally on one side of P’s plane 5) The bounding rectangles of Q and P
do not intersect in the projection plane
Depth Sort (Painter Algorithm)
• If all the above conditions do not hold, P and Q may be split along intersection edge
into two smaller polygons
As was mentioned before, the painter's algorithm is a simplified version of the depth-sort algorithm. In the depth-sort algorithm, there are 3 steps that are performed:
Step 1:Sort objects from near to far (smallest to largest z coordinate).
Step 2:Resolve ambiguities, rearranging the object list and splitting faces as necessary.
Step 3:Render each face on the rearranged list in ascending order of smallest z coordinate (from back to front).
Resolving ambiguities in Step 2 is what replaces simple rendering of the whole face of the object. Let the object farthest away be called P. Before this object is rendered, it must be tested against other objects which we will call Q, where the z extent of q overlaps the z extent of P. This is done to prove that P cannot obscure Q and that P can therefore be written before Q. Up to 5 tests are performed, in order of increasing complexity (Taken from Foley, Van Dam, Feiner, Hughes, Phillips. Introduction to Computer Graphics Addison-Wesley, New York, c.1994):
1. Do the polygons' x extents not overlap?
2. Do the polygons' y extents not overlap?
3. Is P entirely on the opposite side of Q's plane from the viewpoint?
4. Is Q entirely on the same side of P's plane as the viewpoint?
5. Do the projections of the polygons onto the (x,y) plane not overlap? (This can be determined by comparing the edges of one object to the edges of another).
If all 5 tests fail, the assumption is that P obscures Q. So we test whether Q could be rendered before P. Tests 3 and 4 are performed again, with the polygons reversed:
3'. Is Q entirely on the opposite side of P's plane from the viewpoint?
4'. Is P entirely on the same side of Q's plane as the viewpoint?
The next picture is a top down view, relative to th eviewpoint, of objects P and Q.
In this case, test 3' succeeds. So, we move Q to the end of the list of objects, and the old Q becomes the new P.
The next picture is a front view. The tests are inconclusive: The objects intersect each other.
No matter which is P or Q, there is no order in which P and Q could be rendered correctly. Instead, either P or Q must be split by the plane of the other. The original unsplit object is discarded, its pieces are inserted in the list in proper order, and the algorithm proceeds as before. The following picture shows an example of splitting: (taken from http://www.cs.unc.edu/~stewart/comp236/hidden-surface2.html)
The next picture shows a more subtle case: it is possible to move each object to the end of the list to place in the correct order relative to one, but not both, of the other objects.
This would result in an infinite loop. To avoid looping, the object that moves to the end of the list are marked. If the first 5 tests fail and the current Q is marked, tests 3' and 4' are not performed. Instead, one of the objects is split, as if tests 3' and 4' had both failed, and the pieces are reinserted into the list.
a) Explain the Z-buffer algorithm for removing hidden surfaces. [9]
The basic idea is to test the z - depth of each surface to determine the closest (visible) surface. Declare an array z buffer(x, y) with one entry for each pixel position. Initialize the array to the maximum depth. Note: if have performed a perspective depth transformation then all z values 0.0 <= z (x, y) <="1.0". So initialize all values to 1.0. Then the algorithm is as follows:
for each polygon P
for each pixel (x, y) in P
compute z_depth at x, y
if z_depth < z_buffer (x, y) then
set_pixel (x, y, color)
z_buffer (x, y) <= z_depth
The polyscan procedure can easily be modified to add the z-buffer test. The computation of the z_depth (x, y) is done using coherence calculations similar to the x-intersection calculations. It is actually a bi-linear interpolation, i.e., interpolation both down (y) and across (x) scan lines.
Advantages of z-buffer algorithm: It always works and is simple to implement.
Disadvantages:
• May paint the same pixel several times and computing the color of a pixel may be expensive. So might compute the color only if it passes the z_buffer test. Might sort the polygons and scan front to back (reverse of painter's algorithm) - this still tests all the polygons but avoids the expense of computing the intensity and writing it to the frame buffer.
• Large memory requirements: if used real (4 bytes) then for 640 x 480 resolution: 4bytes/pixel = 1,228,000 bytes. We usually use a 24-bit z-buffer so 900,000 bytes or 16 - bit z-buffer = 614,000 bytes. Note: For VGA mode 19 (320 x 200 and only use 240 x 200) then need only 96,000 bytes for a 16-bit z_buffer. However, may need additional z - buffers for special effects, e.g. shadows.
Alternative method for computing z depth values using plane equations.
1. Perform a perspective depth transformation (to maintain planes).
2. Compute plane equations (not the same as before the perspective transformation)
3. For each pixel in PDC (xp, yp) find the x , y wdc values (using an inverse point transform)
4. Put x, y into plane equation to find z in wdc
5. Perform z buffer test on z.
b) What do you mean by hidden lines and surfaces? Describe area subdivision method for removing hidden surfaces. [12]
Area Subdivision Algorithms
The area-subdivision method takes advantage of area coherence in a scene by locating those view
areas that represent part of a single surface.
The total viewing area is successively divided into smaller and smaller rectangles until each small
area is simple, ie. it is a single pixel, or is covered wholly by a part of a single visible surface or no
surface at all.
The procedure to determine whether we should subdivide an area into smaller rectangle is:
1. We first classify each of the surfaces, according to their relations with the area:
Surrounding surface - a single surface completely encloses the area
Overlapping surface - a single surface that is partly inside and partly outside the area
Inside surface - a single surface that is completely inside the area
Outside surface - a single surface that is completely outside the area.
To improve the speed of classification, we can make use of the bounding rectangles of surfaces for
early confirmation or rejection that the surfaces should be belong to that type.
2. Check the result from 1., that, if any of the following condition is true, then, no subdivision of this
area is needed.
a. All surfaces are outside the area.
b. Only one surface is inside, overlapping or surrounding surface is in the area.
c. A surrounding surface obscures all other surfaces within the area boundaries.
For cases b and c, the color of the area can be determined from that single surface.
Rotations in space are more complex, because we can either rotate about the x-axis, the y-axis or the z-axis. When rotating about the z-axis, only coordinates of x and y will change and the z-coordinate will be the same. In effect, it is exactly a rotation about the origin in the xy-plane. Therefore, the rotation equation is
With this set of equations, letting a be 90 degree rotates (1,0,0) to (0,1,0) and (0,1,0) to (-1,0,0). Therefore, the x-axis rotates to the y-axis and the y-axis rotates to the negative direction of the original x-axis. This is the effect of rotating about the z-axis 90 degree.
Based on the same idea, rotating about the x-axis an angle a is the following:
Let us verify the above again with a being 90 degree. This rotates (0,1,0) to (0,0,1) and (0,0,1) to (0,-1,0). Thus, the y-axis rotates to the z-axis and the z-axis rotates to the negative direction of the original y-axis.
But, rotating about the y-axis is different! It is because the way of measuring angles. In a right-handed system, if your right hand holds a coordinate axis with your thumb pointing in the positive direction, your other four fingers give the positive direction of angle measuring. More precisely, the positive direction for measuring angles is from the z-axis to x-axis. However, traditionally the angle measure is from the x-axis to the z-axis. As a result, rotating an angle a about the y-axis in the sense of a right-handed system is equivalent to rotating an angle -a measuring from the x-axis to the z-axis. Therefore, the rotation equations are
Let us verify the above with rotating about the y-axis 90 degree. This rotates (1,0,0) to (0,0,-1) and (0,0,1) to (1,0,0). Therefore, the x-axis rotates to the negative direction of the z-axis and the z-axis rotates to the original x-axis.
A rotation matrix and a translation matrix can be combined into a single matrix as follows, where the r's in the upper-left 3-by-3 matrix form a rotation and p, q and r form a translation vector. This matrix represents rotations followed by a translation.
You can apply this transformation to a plane and a quadric surface just as what we did for lines and conics earlier.
b) Describe the Sutherland-Cohen algorithm for clipping? Is this applicable to any type of window? Justify your answer. [9]
The Cohen-Sutherland Line-Clipping Algorithm
The more efficient Cohen-Sutherland Algorithm performs initial tests on a line to determine whether intersection calculations can be avoided.
Steps for Cohen-Sutherland algorithm
1. End-points pairs are check for trivial acceptance or trivial rejected using the outcode.
2. If not trivial-accepance or trivial-rejected, divided into two segments at a clip edge.
3. Iteratively clipped by testing trivial-acceptance or trivial-rejected, and divided into two segments until completely inside or trivial-rejected.
Pseudo-code of Cohen-Sutherland Algorithm.
Trivial acceptance/reject test
To perform trivial accept and reject tests, we extend the edges of the clip rectangle to divide the plane of the clip rectangle into nine regions. Each region is assigned a 4-bit code deteermined by where the region lies with respect to the outside halfplanes of the clip-rectangle edges. Each bit in the outcode is set to either 1 (true) or 0 (false); the 4 bits in the code correspond to the following conditions:
o Bit 1 : outside halfplane of top edge, above top edge
Y > Ymax
o Bit 2 : outside halfplane of bottom edge, below bottom edge
Y < Ymin
o Bit 3 : outside halfplane of right edge, to the right of right edge
X > Xmax
o Bit 4 : outside halfplane of left edge, to the left of left edge
X < Xmin
Conclusion
In summary, the C-S algorithm is efficient when outcode testing can be done cheaply (for example, by doing bitwise operations in assembly language) and trivial acceptance or rejection is applicable to the majority of line segments .(For example, large windows - everything is inside , or small windows - everything is outside).
3.b) Explain the steps of the Cyrus-Beck line-clipping algorithm. [6]
The Cyrus–Beck algorithm is a line clipping algorithm. It was designed to be more efficient than the Sutherland–Cohen algorithm which uses repetitive clipping [1]. Cyrus–Beck is a general algorithm and can be used with a convex polygon clipping window unlike Sutherland-Cohen that can be used only on a rectangular clipping area
Here the parametric equation of a line in the view plane is:
P(t) = P(0) + t(P1 − P0)
where t = 0 at P(1) t = o at t0
Now to find intersection point with the clipping window we calculate value of dot product
n(Pt-f)
{if > 0 vector pointed toward interior
if = 0 vector pointed parallel to plane containing f
if < 0 vector pointed away from interior
here n stands for normal.
By this we select the point of intersection of line and clipping window where (dot product = 0 ) and hence clip the line
c) Why clipping Is an Important operation for rendering? [4]
b) Is it necessary to compute lighting information before clipping for rendering a 3D scene? Explain. [6]
Geometry in the complete 3D scene is lit according to the defined locations of light sources and reflectance and other surface properties. Current hardware implementations of the graphics pipeline compute lighting only at the vertices of the polygons being rendered. The lighting values between vertices are then interpolated during rasterization. Per-fragment (i.e. per-pixel) lighting can be done on modern graphics hardware as a post-rasterization process by means of a shader program.
.Outline the steps required to generate a hidden-surface image using the depth-buffer approach and then comment on the relative merits of this approach compared with the scan-line algorithm. [18]
Comparison of Visibility Algorithms
ray casting:
memory: used for object database
implementation: easy, but to make it fast you need spatial data structures
speed: slow if many objects: cost is O((#pixels)´(#objects))
generality: excellent, can even do CSG (constructive solid geometry), shadows, transp.
painter’s:
memory: used for image buffer
implementation: moderate, requires scan conversion; hard if sorting & splitting needed
speed: fast if objects can be sorted a priori, otherwise sorting many objs. can be costly
generality: splitting of intersecting objects & sorting make it clumsy for general 3-D rendering
z-buffer:
memory: used for image buffer & z-buffer
implementation: moderate, requires scan conversion. It can be put in hardware.
speed: fast, unless depth complexity is high (redundant shading)
generality: very good
others (scanline, object space): tend to be hard to implement, and very hard to generalize to non-polygon models
c) Describe the features of Depths sort algorithm. [6]
It is one solution to the visibility problem, which is the problem of deciding which elements of a rendered scene are visible, and which are hidden. The painter's algorithm is another common solution which, though less efficient, can also handle non-opaque scene elements. Z-buffering is also known as depth buffering.
Algorithm:
• Sort the polygons in the scene by their depth
• Draw them back to front
• Problem: Unless all polygons have constant z, a strict depth ordering may not exist
Note: Constant z case is important in VLSI design
Depth Sort (Painter Algorithm)
• General Case: Given two polygons P and Q, an order may be determined between them, if at least
one of the following holds:
1) z values of P and Q do not overlap 2) The bounding rectangle in the x, y plane for P and Q do not overlap
3) P is totally on one side of Q’s plane 4) Q is totally on one side of P’s plane 5) The bounding rectangles of Q and P
do not intersect in the projection plane
Depth Sort (Painter Algorithm)
• If all the above conditions do not hold, P and Q may be split along intersection edge
into two smaller polygons
As was mentioned before, the painter's algorithm is a simplified version of the depth-sort algorithm. In the depth-sort algorithm, there are 3 steps that are performed:
Step 1:Sort objects from near to far (smallest to largest z coordinate).
Step 2:Resolve ambiguities, rearranging the object list and splitting faces as necessary.
Step 3:Render each face on the rearranged list in ascending order of smallest z coordinate (from back to front).
Resolving ambiguities in Step 2 is what replaces simple rendering of the whole face of the object. Let the object farthest away be called P. Before this object is rendered, it must be tested against other objects which we will call Q, where the z extent of q overlaps the z extent of P. This is done to prove that P cannot obscure Q and that P can therefore be written before Q. Up to 5 tests are performed, in order of increasing complexity (Taken from Foley, Van Dam, Feiner, Hughes, Phillips. Introduction to Computer Graphics Addison-Wesley, New York, c.1994):
1. Do the polygons' x extents not overlap?
2. Do the polygons' y extents not overlap?
3. Is P entirely on the opposite side of Q's plane from the viewpoint?
4. Is Q entirely on the same side of P's plane as the viewpoint?
5. Do the projections of the polygons onto the (x,y) plane not overlap? (This can be determined by comparing the edges of one object to the edges of another).
If all 5 tests fail, the assumption is that P obscures Q. So we test whether Q could be rendered before P. Tests 3 and 4 are performed again, with the polygons reversed:
3'. Is Q entirely on the opposite side of P's plane from the viewpoint?
4'. Is P entirely on the same side of Q's plane as the viewpoint?
The next picture is a top down view, relative to th eviewpoint, of objects P and Q.
In this case, test 3' succeeds. So, we move Q to the end of the list of objects, and the old Q becomes the new P.
The next picture is a front view. The tests are inconclusive: The objects intersect each other.
No matter which is P or Q, there is no order in which P and Q could be rendered correctly. Instead, either P or Q must be split by the plane of the other. The original unsplit object is discarded, its pieces are inserted in the list in proper order, and the algorithm proceeds as before. The following picture shows an example of splitting: (taken from http://www.cs.unc.edu/~stewart/comp236/hidden-surface2.html)
The next picture shows a more subtle case: it is possible to move each object to the end of the list to place in the correct order relative to one, but not both, of the other objects.
This would result in an infinite loop. To avoid looping, the object that moves to the end of the list are marked. If the first 5 tests fail and the current Q is marked, tests 3' and 4' are not performed. Instead, one of the objects is split, as if tests 3' and 4' had both failed, and the pieces are reinserted into the list.
a) Explain the Z-buffer algorithm for removing hidden surfaces. [9]
The basic idea is to test the z - depth of each surface to determine the closest (visible) surface. Declare an array z buffer(x, y) with one entry for each pixel position. Initialize the array to the maximum depth. Note: if have performed a perspective depth transformation then all z values 0.0 <= z (x, y) <="1.0". So initialize all values to 1.0. Then the algorithm is as follows:
for each polygon P
for each pixel (x, y) in P
compute z_depth at x, y
if z_depth < z_buffer (x, y) then
set_pixel (x, y, color)
z_buffer (x, y) <= z_depth
The polyscan procedure can easily be modified to add the z-buffer test. The computation of the z_depth (x, y) is done using coherence calculations similar to the x-intersection calculations. It is actually a bi-linear interpolation, i.e., interpolation both down (y) and across (x) scan lines.
Advantages of z-buffer algorithm: It always works and is simple to implement.
Disadvantages:
• May paint the same pixel several times and computing the color of a pixel may be expensive. So might compute the color only if it passes the z_buffer test. Might sort the polygons and scan front to back (reverse of painter's algorithm) - this still tests all the polygons but avoids the expense of computing the intensity and writing it to the frame buffer.
• Large memory requirements: if used real (4 bytes) then for 640 x 480 resolution: 4bytes/pixel = 1,228,000 bytes. We usually use a 24-bit z-buffer so 900,000 bytes or 16 - bit z-buffer = 614,000 bytes. Note: For VGA mode 19 (320 x 200 and only use 240 x 200) then need only 96,000 bytes for a 16-bit z_buffer. However, may need additional z - buffers for special effects, e.g. shadows.
Alternative method for computing z depth values using plane equations.
1. Perform a perspective depth transformation (to maintain planes).
2. Compute plane equations (not the same as before the perspective transformation)
3. For each pixel in PDC (xp, yp) find the x , y wdc values (using an inverse point transform)
4. Put x, y into plane equation to find z in wdc
5. Perform z buffer test on z.
b) What do you mean by hidden lines and surfaces? Describe area subdivision method for removing hidden surfaces. [12]
Area Subdivision Algorithms
The area-subdivision method takes advantage of area coherence in a scene by locating those view
areas that represent part of a single surface.
The total viewing area is successively divided into smaller and smaller rectangles until each small
area is simple, ie. it is a single pixel, or is covered wholly by a part of a single visible surface or no
surface at all.
The procedure to determine whether we should subdivide an area into smaller rectangle is:
1. We first classify each of the surfaces, according to their relations with the area:
Surrounding surface - a single surface completely encloses the area
Overlapping surface - a single surface that is partly inside and partly outside the area
Inside surface - a single surface that is completely inside the area
Outside surface - a single surface that is completely outside the area.
To improve the speed of classification, we can make use of the bounding rectangles of surfaces for
early confirmation or rejection that the surfaces should be belong to that type.
2. Check the result from 1., that, if any of the following condition is true, then, no subdivision of this
area is needed.
a. All surfaces are outside the area.
b. Only one surface is inside, overlapping or surrounding surface is in the area.
c. A surrounding surface obscures all other surfaces within the area boundaries.
For cases b and c, the color of the area can be determined from that single surface.
No comments:
Post a Comment
Note: Only a member of this blog may post a comment.